Oscillatory system with 1:1:1 internal resonance
Contents
We extract FRC of a three DOFs model with 1:1:1 internal resonance
clear all, close all, clc
Example Setup
epsilon = 5e-3; c1 = 5e-4; c2 = 1e-3; c3 = 1.5e-3; K = 1e-3; [mass,damp,stiff,fnl,fext]=build_model(c1,c2,c3,K);
Dynamical System Setup
order = 2; DS = DynamicalSystem(order); set(DS,'M',mass,'C',damp,'K',stiff,'fnl',fnl); set(DS.Options,'Emax',5,'Nmax',10,'notation','multiindex')
Forcing
kappas = [1; -1]; coeffs = [fext fext]/2; DS.add_forcing(coeffs, kappas, epsilon);
Linear Modal analysis
startMD = tic; [V,D,W] = DS.linear_spectral_analysis(); timings.MD = toc(startMD);
The first 6 nonzero eigenvalues are given as -0.0002 + 1.0000i -0.0002 - 1.0000i -0.0005 + 1.0000i -0.0005 - 1.0000i -0.0008 + 1.0000i -0.0008 - 1.0000i
6D SSM based computation
1:1:1 internal resonance
S = SSM(DS); set(S.Options, 'reltol', 1,'notation','multiindex'); order = 3; outdof = [1 2 3];
We are interested in the FRC over the frequency span [0.995 1.016]. We can call the routine extract_FRC to extract the FRC. All the three natural frequencies are inside the frequency span. The frequency span is divided into a single subinterval because of the 1:1:1 internal resonance. A single continuation run is involved to get the FRC for the subinterval.
set(S.Options, 'IRtol',0.02,'notation', 'multiindex','contribNonAuto',true) set(S.FRCOptions, 'method','continuation ep') set(S.FRCOptions, 'outdof',outdof) set(S.FRCOptions, 'initialSolver', 'fsolve'); set(S.contOptions,'PtMX',250); freqRange = [0.995 1.016];
call extract_FRC to calculate the FRC
FRC = S.extract_FRC('freq',freqRange,order);
The master subspace has internal resonances: [1 1 1 1 1 1]
*****************************************
Calculating FRC using SSM with master subspace: [1 2 3 4 5 6]
The master subspace contains the following eigenvalues
lambda1 == - 0.00025 + 1i
lambda2 == (-0.00025) - 1i
lambda3 == - 0.0005 + 1i
lambda4 == (-0.0005) - 1i
lambda5 == - 0.00075 + 1i
lambda6 == (-0.00075) - 1i
sigma_out = 0
(near) inner resonance detected for the following combination of master eigenvalues:
1*lambda1 + 0*lambda2 + 0*lambda3 + 0*lambda4 + 1*lambda5 + 0*lambda6 == lambda1
0*lambda1 + 0*lambda2 + 0*lambda3 + 0*lambda4 + 2*lambda5 + 1*lambda6 == lambda1
0*lambda1 + 0*lambda2 + 0*lambda3 + 1*lambda4 + 2*lambda5 + 0*lambda6 == lambda1
.
.
.
sigma_in = 3
Manifold computation time at order 2 = 00:00:00
Estimated memory usage at order 2 = 2.42E-02 MB
Manifold computation time at order 3 = 00:00:00
Estimated memory usage at order 3 = 6.34E-02 MB
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.
Run='freqSubint1.ep': Continue equilibria along primary branch.
STEP DAMPING NORMS COMPUTATION TIMES
IT SIT GAMMA ||d|| ||f|| ||U|| F(x) DF(x) SOLVE
0 2.64e-09 1.07e+01 0.1 0.0 0.0
STEP TIME ||U|| LABEL TYPE om rho1 rho2 rho3 th1 th2 th3 eps
0 00:00:01 1.0746e+01 1 EP 1.0000e+00 2.2254e+00 1.4394e+00 1.0270e+00 4.6046e+00 4.0733e+00 3.2966e+00 5.0000e-03
10 00:00:03 1.1732e+01 2 9.9957e-01 1.8557e+00 9.2553e-01 3.2523e-01 5.0674e+00 4.6994e+00 3.9559e+00 5.0000e-03
20 00:00:04 1.2604e+01 3 9.9826e-01 8.5259e-01 1.4704e-01 1.2288e-03 5.3697e+00 5.1397e+00 4.7363e+00 5.0000e-03
30 00:00:06 1.2935e+01 4 9.9696e-01 5.4610e-01 3.2953e-02 8.5618e-06 5.4199e+00 5.2668e+00 5.0251e+00 5.0000e-03
40 00:00:10 1.3118e+01 5 9.9543e-01 3.7819e-01 8.2670e-03 9.1557e-08 5.4442e+00 5.3376e+00 5.1748e+00 5.0000e-03
44 00:00:11 1.3152e+01 6 EP 9.9500e-01 3.4717e-01 5.9321e-03 3.0968e-08 5.4486e+00 5.3507e+00 5.2018e+00 5.0000e-03
STEP TIME ||U|| LABEL TYPE om rho1 rho2 rho3 th1 th2 th3 eps
0 00:00:11 1.0746e+01 7 EP 1.0000e+00 2.2254e+00 1.4394e+00 1.0270e+00 4.6046e+00 4.0733e+00 3.2966e+00 5.0000e-03
10 00:00:12 9.3792e+00 8 1.0004e+00 1.8553e+00 1.3351e+00 1.3646e+00 4.2110e+00 3.4218e+00 2.5410e+00 5.0000e-03
20 00:00:12 8.3005e+00 9 1.0013e+00 1.5476e+00 7.9066e-01 1.5315e+00 4.1459e+00 2.8535e+00 1.6583e+00 5.0000e-03
30 00:00:13 7.7094e+00 10 1.0024e+00 1.8740e+00 5.3870e-01 1.7407e+00 3.8252e+00 2.5069e+00 9.8178e-01 5.0000e-03
35 00:00:14 7.3392e+00 11 SN 1.0025e+00 1.9151e+00 5.1776e-01 1.6956e+00 3.6010e+00 2.3728e+00 7.2064e-01 5.0000e-03
35 00:00:14 7.3392e+00 12 FP 1.0025e+00 1.9151e+00 5.1776e-01 1.6956e+00 3.6010e+00 2.3728e+00 7.2064e-01 5.0000e-03
40 00:00:14 6.7542e+00 13 1.0023e+00 1.8415e+00 5.3293e-01 1.4787e+00 3.2967e+00 2.2182e+00 3.9337e-01 5.0000e-03
47 00:00:15 5.6193e+00 14 SN 1.0018e+00 1.3918e+00 6.2354e-01 7.8094e-01 2.8362e+00 1.9228e+00 -3.2860e-01 5.0000e-03
47 00:00:15 5.6193e+00 15 FP 1.0018e+00 1.3918e+00 6.2354e-01 7.8094e-01 2.8362e+00 1.9228e+00 -3.2860e-01 5.0000e-03
50 00:00:15 5.3793e+00 16 1.0019e+00 1.1827e+00 6.5459e-01 6.3228e-01 2.7821e+00 1.7508e+00 -6.5770e-01 5.0000e-03
53 00:00:15 5.2836e+00 17 HB 1.0021e+00 1.0124e+00 6.8834e-01 5.6849e-01 2.7797e+00 1.5855e+00 -9.4407e-01 5.0000e-03
60 00:00:16 5.6878e+00 18 1.0040e+00 6.2522e-01 8.9986e-01 5.5065e-01 3.0777e+00 1.1376e+00 -1.7022e+00 5.0000e-03
70 00:00:16 6.6111e+00 19 1.0081e+00 7.0981e-01 1.2679e+00 6.0120e-01 3.6326e+00 9.3088e-01 -2.0740e+00 5.0000e-03
80 00:00:17 7.0282e+00 20 1.0128e+00 1.0047e+00 1.5740e+00 5.8776e-01 3.7558e+00 8.0695e-01 -2.2545e+00 5.0000e-03
88 00:00:17 7.0826e+00 21 HB 1.0150e+00 1.1574e+00 1.6754e+00 5.4840e-01 3.6429e+00 6.4197e-01 -2.4333e+00 5.0000e-03
90 00:00:18 7.0682e+00 22 1.0154e+00 1.1960e+00 1.6839e+00 5.2559e-01 3.5720e+00 5.6103e-01 -2.5165e+00 5.0000e-03
92 00:00:18 7.0527e+00 23 SN 1.0154e+00 1.2126e+00 1.6800e+00 5.1008e-01 3.5265e+00 5.1138e-01 -2.5668e+00 5.0000e-03
92 00:00:18 7.0527e+00 24 FP 1.0154e+00 1.2126e+00 1.6800e+00 5.1008e-01 3.5265e+00 5.1138e-01 -2.5668e+00 5.0000e-03
100 00:00:18 6.7311e+00 25 1.0111e+00 1.1708e+00 1.3243e+00 2.7824e-01 3.0215e+00 1.0008e-02 -3.0496e+00 5.0000e-03
110 00:00:19 6.2183e+00 26 1.0032e+00 7.2928e-01 1.7135e-01 1.1881e-03 2.4710e+00 -4.7512e-01 -3.3815e+00 5.0000e-03
112 00:00:19 6.2195e+00 27 FP 1.0031e+00 7.0250e-01 1.4145e-01 6.6679e-04 2.4638e+00 -4.8721e-01 -3.3931e+00 5.0000e-03
112 00:00:19 6.2195e+00 28 SN 1.0031e+00 7.0250e-01 1.4145e-01 6.6679e-04 2.4638e+00 -4.8721e-01 -3.3931e+00 5.0000e-03
120 00:00:20 6.3051e+00 29 1.0038e+00 4.9450e-01 2.8006e-02 4.2745e-06 2.4266e+00 -5.7608e-01 -3.5219e+00 5.0000e-03
130 00:00:22 6.3960e+00 30 1.0049e+00 3.6535e-01 7.8504e-03 7.2636e-08 2.4079e+00 -6.3060e-01 -3.6215e+00 5.0000e-03
134 00:00:22 6.4220e+00 31 MX 1.0054e+00 3.3244e-01 5.3293e-03 2.0827e-08 2.4032e+00 -6.4451e-01 -3.6481e+00 5.0000e-03
Total time spent on FRC computation upto O(3) = 00:01:00
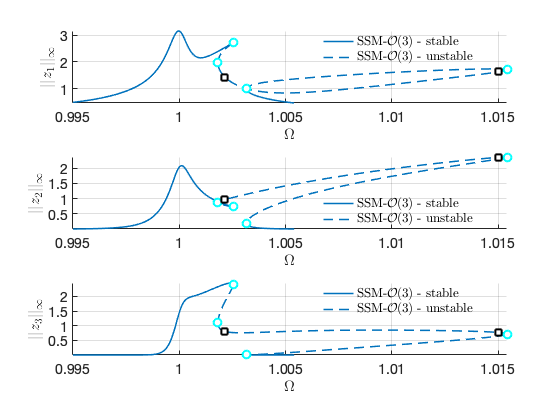
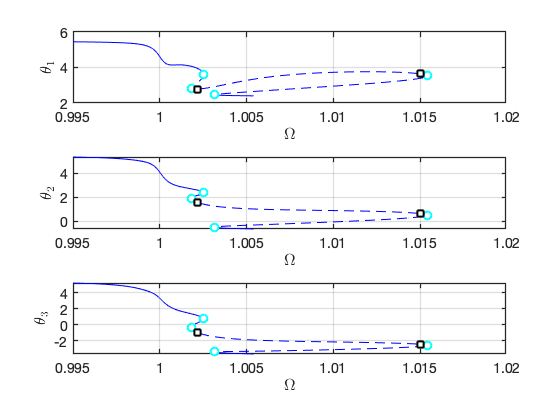
On the other hand, we can use SSM-ep toolbox to obtaint the FRC with a single continuation run as well given in the whole frequency span. The SSM-ep toolbox is the minic of the ep-toolbox of COCO. It is in the middle level of the SSMTool while the extract_FRC routine is in the high level of the SSMTool. The continuation-based method implemented in the extract_FRC routine is actually built on the SSM-ep toolbox. Users may use the extract_FRC routine initially. They may explore the SSM-ep toolbox given this toolbox has more functionalities, e.g., bifurcation analysis.
We call the function SSM_isol2ep, whose arguments can be found via help
help SSM_isol2ep
--- help for SSM/SSM_isol2ep ---
SSM_ISOL2EP This function performs continuation of equilibrium points of
slow dynamics. Each equilibirum point corresponds to a periodic orbit in
the regular time dynamics. The continuation here starts from the guess of
initial solution.
FRC = SSM_ISOL2EP(OBJ,OID,RESONANT_MODES,ORDER,MFREQS,PARNAME,PARRANGE,OUTDOF,VARARGIN)
oid: runid of continuation
resonant_modes: master subspace
order: expansion order of SSM
mFreqs: internal resonance relation vector
parName: amp/freq continuation parameter
parRange: continuation domain of parameter, which should be near the
value of natural frequency with index 1 in the mFreq if the continuation
parameter is freq
outdof: output for dof in physical domain
varargin: [{p0,z0}], ['saveICs'] where {p0,z0} are initial solution
guesses and saveICs is a flag saving a point on trajectory as initial
condition for numerical integration
In this example, the resonant_modes should be [1 2 3 4 5 6] due to all modes are involved in the resonance. We have and then (mfreqs). The argument parName can be amp or freq. When parName='freq'/'amp', the forced response curve with varied excitation frequency / excitation amplitude is obtained.
resonant_modes = [1 2 3 4 5 6]; mFreq = [1 1 1]; set(S.contOptions,'PtMX',250); startep = tic; FRC_ep_polar = S.SSM_isol2ep('isol_polar',resonant_modes, order, mFreq, 'freq', freqRange, outdof); timings.epPolarFRC = toc(startep);
The master subspace contains the following eigenvalues
lambda1 == - 0.00025 + 1i
lambda2 == (-0.00025) - 1i
lambda3 == - 0.0005 + 1i
lambda4 == (-0.0005) - 1i
lambda5 == - 0.00075 + 1i
lambda6 == (-0.00075) - 1i
sigma_out = 0
(near) inner resonance detected for the following combination of master eigenvalues:
1*lambda1 + 0*lambda2 + 0*lambda3 + 0*lambda4 + 1*lambda5 + 0*lambda6 == lambda1
0*lambda1 + 0*lambda2 + 0*lambda3 + 0*lambda4 + 2*lambda5 + 1*lambda6 == lambda1
0*lambda1 + 0*lambda2 + 0*lambda3 + 1*lambda4 + 2*lambda5 + 0*lambda6 == lambda1
.
.
.
sigma_in = 3
Manifold computation time at order 2 = 00:00:00
Estimated memory usage at order 2 = 2.42E-02 MB
Manifold computation time at order 3 = 00:00:01
Estimated memory usage at order 3 = 6.34E-02 MB
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.
Run='isol_polar.ep': Continue equilibria along primary branch.
STEP DAMPING NORMS COMPUTATION TIMES
IT SIT GAMMA ||d|| ||f|| ||U|| F(x) DF(x) SOLVE
0 2.64e-09 1.07e+01 0.0 0.0 0.0
STEP TIME ||U|| LABEL TYPE om rho1 rho2 rho3 th1 th2 th3 eps
0 00:00:00 1.0746e+01 1 EP 1.0000e+00 2.2254e+00 1.4394e+00 1.0270e+00 4.6046e+00 4.0733e+00 3.2966e+00 5.0000e-03
10 00:00:01 1.1732e+01 2 9.9957e-01 1.8557e+00 9.2553e-01 3.2523e-01 5.0674e+00 4.6994e+00 3.9559e+00 5.0000e-03
20 00:00:02 1.2604e+01 3 9.9826e-01 8.5259e-01 1.4704e-01 1.2288e-03 5.3697e+00 5.1397e+00 4.7363e+00 5.0000e-03
30 00:00:05 1.2935e+01 4 9.9696e-01 5.4610e-01 3.2953e-02 8.5618e-06 5.4199e+00 5.2668e+00 5.0251e+00 5.0000e-03
40 00:00:07 1.3118e+01 5 9.9543e-01 3.7819e-01 8.2670e-03 9.1557e-08 5.4442e+00 5.3376e+00 5.1748e+00 5.0000e-03
44 00:00:08 1.3152e+01 6 EP 9.9500e-01 3.4717e-01 5.9321e-03 3.0968e-08 5.4486e+00 5.3507e+00 5.2018e+00 5.0000e-03
STEP TIME ||U|| LABEL TYPE om rho1 rho2 rho3 th1 th2 th3 eps
0 00:00:08 1.0746e+01 7 EP 1.0000e+00 2.2254e+00 1.4394e+00 1.0270e+00 4.6046e+00 4.0733e+00 3.2966e+00 5.0000e-03
10 00:00:08 9.3792e+00 8 1.0004e+00 1.8553e+00 1.3351e+00 1.3646e+00 4.2110e+00 3.4218e+00 2.5410e+00 5.0000e-03
20 00:00:10 8.3005e+00 9 1.0013e+00 1.5476e+00 7.9066e-01 1.5315e+00 4.1459e+00 2.8535e+00 1.6583e+00 5.0000e-03
30 00:00:11 7.7094e+00 10 1.0024e+00 1.8740e+00 5.3870e-01 1.7407e+00 3.8252e+00 2.5069e+00 9.8178e-01 5.0000e-03
35 00:00:13 7.3392e+00 11 SN 1.0025e+00 1.9151e+00 5.1776e-01 1.6956e+00 3.6010e+00 2.3728e+00 7.2064e-01 5.0000e-03
35 00:00:13 7.3392e+00 12 FP 1.0025e+00 1.9151e+00 5.1776e-01 1.6956e+00 3.6010e+00 2.3728e+00 7.2064e-01 5.0000e-03
40 00:00:13 6.7542e+00 13 1.0023e+00 1.8415e+00 5.3293e-01 1.4787e+00 3.2967e+00 2.2182e+00 3.9337e-01 5.0000e-03
47 00:00:14 5.6193e+00 14 SN 1.0018e+00 1.3918e+00 6.2354e-01 7.8094e-01 2.8362e+00 1.9228e+00 -3.2860e-01 5.0000e-03
47 00:00:14 5.6193e+00 15 FP 1.0018e+00 1.3918e+00 6.2354e-01 7.8094e-01 2.8362e+00 1.9228e+00 -3.2860e-01 5.0000e-03
50 00:00:14 5.3793e+00 16 1.0019e+00 1.1827e+00 6.5459e-01 6.3228e-01 2.7821e+00 1.7508e+00 -6.5770e-01 5.0000e-03
53 00:00:14 5.2836e+00 17 HB 1.0021e+00 1.0124e+00 6.8834e-01 5.6849e-01 2.7797e+00 1.5855e+00 -9.4407e-01 5.0000e-03
60 00:00:14 5.6878e+00 18 1.0040e+00 6.2522e-01 8.9986e-01 5.5065e-01 3.0777e+00 1.1376e+00 -1.7022e+00 5.0000e-03
70 00:00:15 6.6111e+00 19 1.0081e+00 7.0981e-01 1.2679e+00 6.0120e-01 3.6326e+00 9.3088e-01 -2.0740e+00 5.0000e-03
80 00:00:16 7.0282e+00 20 1.0128e+00 1.0047e+00 1.5740e+00 5.8776e-01 3.7558e+00 8.0695e-01 -2.2545e+00 5.0000e-03
88 00:00:16 7.0826e+00 21 HB 1.0150e+00 1.1574e+00 1.6754e+00 5.4840e-01 3.6429e+00 6.4197e-01 -2.4333e+00 5.0000e-03
90 00:00:16 7.0682e+00 22 1.0154e+00 1.1960e+00 1.6839e+00 5.2559e-01 3.5720e+00 5.6103e-01 -2.5165e+00 5.0000e-03
92 00:00:16 7.0527e+00 23 SN 1.0154e+00 1.2126e+00 1.6800e+00 5.1008e-01 3.5265e+00 5.1138e-01 -2.5668e+00 5.0000e-03
92 00:00:16 7.0527e+00 24 FP 1.0154e+00 1.2126e+00 1.6800e+00 5.1008e-01 3.5265e+00 5.1138e-01 -2.5668e+00 5.0000e-03
100 00:00:17 6.7311e+00 25 1.0111e+00 1.1708e+00 1.3243e+00 2.7824e-01 3.0215e+00 1.0008e-02 -3.0496e+00 5.0000e-03
110 00:00:17 6.2183e+00 26 1.0032e+00 7.2928e-01 1.7135e-01 1.1881e-03 2.4710e+00 -4.7512e-01 -3.3815e+00 5.0000e-03
112 00:00:18 6.2195e+00 27 FP 1.0031e+00 7.0250e-01 1.4145e-01 6.6679e-04 2.4638e+00 -4.8721e-01 -3.3931e+00 5.0000e-03
112 00:00:18 6.2195e+00 28 SN 1.0031e+00 7.0250e-01 1.4145e-01 6.6679e-04 2.4638e+00 -4.8721e-01 -3.3931e+00 5.0000e-03
120 00:00:18 6.3051e+00 29 1.0038e+00 4.9450e-01 2.8006e-02 4.2745e-06 2.4266e+00 -5.7608e-01 -3.5219e+00 5.0000e-03
130 00:00:20 6.3960e+00 30 1.0049e+00 3.6535e-01 7.8504e-03 7.2636e-08 2.4079e+00 -6.3060e-01 -3.6215e+00 5.0000e-03
134 00:00:21 6.4220e+00 31 MX 1.0054e+00 3.3244e-01 5.3293e-03 2.0827e-08 2.4032e+00 -6.4451e-01 -3.6481e+00 5.0000e-03
the forcing frequency 9.9500e-01 is nearly resonant with the eigenvalue -2.5000e-04 + i1.0000e+00
the forcing frequency 9.9501e-01 is nearly resonant with the eigenvalue -2.5000e-04 + i1.0000e+00
the forcing frequency 9.9515e-01 is nearly resonant with the eigenvalue -2.5000e-04 + i1.0000e+00
.
.
.

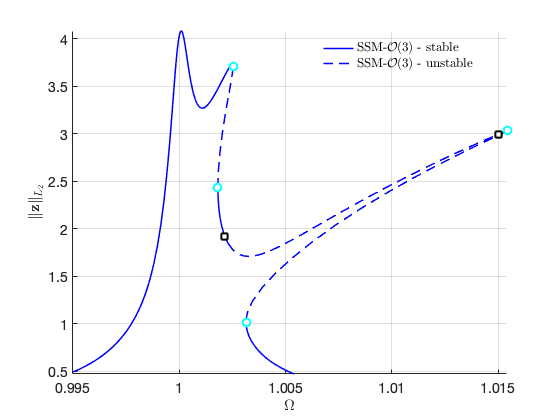
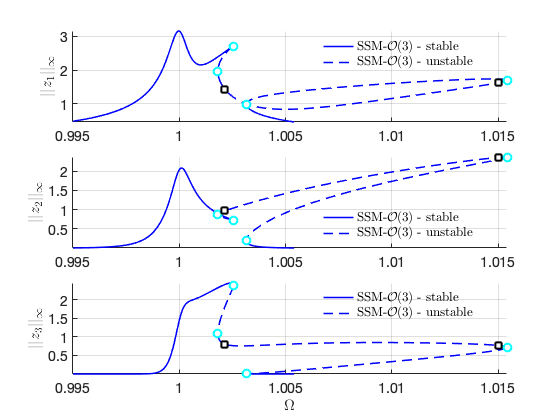
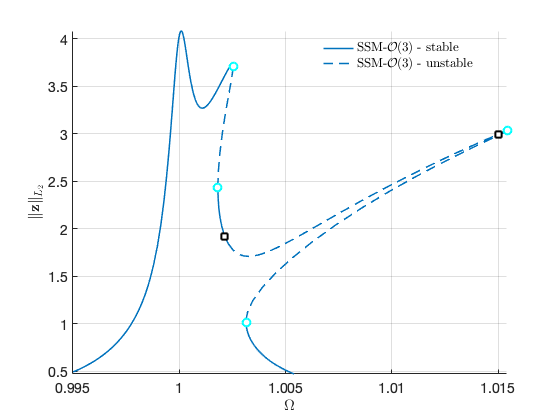
As seen in the continuation hisotry, the continuation run terminated at a point where (denoted as MX point), which triggers the singularity of the vector field. As an alternative, we can use Cartesian coordinates to remove the MX point.
set(S.FRCOptions, 'coordinates','cartesian'); startep = tic; FRC_ep_cart = S.SSM_isol2ep('isol_cart',resonant_modes, order, mFreq, 'freq', freqRange, outdof); timings.epCartFRC = toc(startep);
The master subspace contains the following eigenvalues
lambda1 == - 0.00025 + 1i
lambda2 == (-0.00025) - 1i
lambda3 == - 0.0005 + 1i
lambda4 == (-0.0005) - 1i
lambda5 == - 0.00075 + 1i
lambda6 == (-0.00075) - 1i
sigma_out = 0
(near) inner resonance detected for the following combination of master eigenvalues:
1*lambda1 + 0*lambda2 + 0*lambda3 + 0*lambda4 + 1*lambda5 + 0*lambda6 == lambda1
0*lambda1 + 0*lambda2 + 0*lambda3 + 0*lambda4 + 2*lambda5 + 1*lambda6 == lambda1
0*lambda1 + 0*lambda2 + 0*lambda3 + 1*lambda4 + 2*lambda5 + 0*lambda6 == lambda1
.
.
.
sigma_in = 3
Manifold computation time at order 2 = 00:00:00
Estimated memory usage at order 2 = 2.42E-02 MB
Manifold computation time at order 3 = 00:00:00
Estimated memory usage at order 3 = 6.34E-02 MB
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.
Run='isol_cart.ep': Continue equilibria along primary branch.
STEP DAMPING NORMS COMPUTATION TIMES
IT SIT GAMMA ||d|| ||f|| ||U|| F(x) DF(x) SOLVE
0 1.76e-08 4.26e+00 0.0 0.0 0.0
STEP TIME ||U|| LABEL TYPE om Rez1 Rez2 Rez3 Imz1 Imz2 Imz3 eps
0 00:00:00 4.2612e+00 1 EP 1.0000e+00 -2.3952e-01 -8.5858e-01 -1.0146e+00 -2.2125e+00 -1.1553e+00 -1.5853e-01 5.0000e-03
10 00:00:00 3.8345e+00 2 9.9978e-01 3.6271e-01 -3.0857e-01 -5.3949e-01 -2.0866e+00 -1.1706e+00 -3.3148e-01 5.0000e-03
20 00:00:00 2.9882e+00 3 9.9944e-01 7.0384e-01 6.7160e-02 -1.1843e-01 -1.5306e+00 -7.6358e-01 -1.6172e-01 5.0000e-03
30 00:00:01 1.8567e+00 4 9.9823e-01 5.1524e-01 5.9059e-02 3.7431e-05 -6.6464e-01 -1.2809e-01 -1.0694e-03 5.0000e-03
36 00:00:01 1.4904e+00 5 EP 9.9500e-01 2.3313e-01 3.5345e-03 1.4557e-08 -2.5725e-01 -4.7642e-03 -2.7333e-08 5.0000e-03
STEP TIME ||U|| LABEL TYPE om Rez1 Rez2 Rez3 Imz1 Imz2 Imz3 eps
0 00:00:01 4.2612e+00 6 EP 1.0000e+00 -2.3952e-01 -8.5858e-01 -1.0146e+00 -2.2125e+00 -1.1553e+00 -1.5853e-01 5.0000e-03
10 00:00:01 4.2339e+00 7 1.0002e+00 -7.5362e-01 -1.2473e+00 -1.2274e+00 -1.9141e+00 -7.2792e-01 3.7254e-01 5.0000e-03
20 00:00:02 3.8236e+00 8 1.0005e+00 -8.9698e-01 -1.2036e+00 -9.4094e-01 -1.4419e+00 -1.3022e-01 1.0366e+00 5.0000e-03
30 00:00:03 3.5592e+00 9 1.0012e+00 -8.2201e-01 -7.8506e-01 -1.9070e-01 -1.2991e+00 2.1546e-01 1.5064e+00 5.0000e-03
40 00:00:04 3.8572e+00 10 1.0021e+00 -1.1983e+00 -5.0346e-01 6.3364e-01 -1.3216e+00 2.9278e-01 1.5847e+00 5.0000e-03
50 00:00:04 3.9601e+00 11 1.0025e+00 -1.7012e+00 -3.7600e-01 1.2571e+00 -8.7962e-01 3.5660e-01 1.1486e+00 5.0000e-03
51 00:00:05 3.9537e+00 12 FP 1.0025e+00 -1.7166e+00 -3.7213e-01 1.2740e+00 -8.4917e-01 3.6000e-01 1.1188e+00 5.0000e-03
51 00:00:05 3.9537e+00 13 SN 1.0025e+00 -1.7166e+00 -3.7213e-01 1.2740e+00 -8.4917e-01 3.6000e-01 1.1188e+00 5.0000e-03
60 00:00:05 3.5811e+00 14 1.0022e+00 -1.7895e+00 -3.0942e-01 1.3195e+00 -1.0986e-01 4.4862e-01 3.9369e-01 5.0000e-03
70 00:00:06 2.8554e+00 15 1.0018e+00 -1.3644e+00 -2.2659e-01 7.8156e-01 4.0878e-01 5.7576e-01 -2.2459e-01 5.0000e-03
71 00:00:06 2.8069e+00 16 FP 1.0018e+00 -1.3274e+00 -2.1501e-01 7.3916e-01 4.1851e-01 5.8530e-01 -2.5202e-01 5.0000e-03
71 00:00:06 2.8069e+00 17 SN 1.0018e+00 -1.3274e+00 -2.1501e-01 7.3916e-01 4.1852e-01 5.8530e-01 -2.5202e-01 5.0000e-03
78 00:00:07 2.3775e+00 18 HB 1.0021e+00 -9.4682e-01 -1.0152e-02 3.3342e-01 3.5840e-01 6.8827e-01 -4.6045e-01 5.0000e-03
80 00:00:08 2.2434e+00 19 1.0027e+00 -7.7003e-01 1.5267e-01 1.3824e-01 2.3768e-01 7.4124e-01 -5.1945e-01 5.0000e-03
90 00:00:08 2.5861e+00 20 1.0075e+00 -6.1339e-01 7.2060e-01 -2.7633e-01 -2.9691e-01 9.9355e-01 -5.3079e-01 5.0000e-03
100 00:00:09 3.1443e+00 21 1.0131e+00 -8.4021e-01 1.1151e+00 -3.7651e-01 -5.8521e-01 1.1327e+00 -4.4736e-01 5.0000e-03
109 00:00:10 3.3099e+00 22 HB 1.0150e+00 -1.0150e+00 1.3419e+00 -4.1650e-01 -5.5617e-01 1.0032e+00 -3.5674e-01 5.0000e-03
110 00:00:10 3.3286e+00 23 1.0152e+00 -1.0540e+00 1.3883e+00 -4.2254e-01 -5.2912e-01 9.5003e-01 -3.3136e-01 5.0000e-03
114 00:00:11 3.3419e+00 24 SN 1.0154e+00 -1.1239e+00 1.4651e+00 -4.2812e-01 -4.5529e-01 8.2217e-01 -2.7730e-01 5.0000e-03
114 00:00:11 3.3419e+00 25 FP 1.0154e+00 -1.1239e+00 1.4651e+00 -4.2812e-01 -4.5529e-01 8.2217e-01 -2.7730e-01 5.0000e-03
120 00:00:11 3.2306e+00 26 1.0143e+00 -1.2209e+00 1.5216e+00 -3.9259e-01 -1.8470e-01 4.2070e-01 -1.3714e-01 5.0000e-03
130 00:00:12 2.7344e+00 27 1.0095e+00 -1.0966e+00 1.1812e+00 -2.1764e-01 2.5256e-01 -1.0311e-01 -1.3893e-03 5.0000e-03
140 00:00:12 2.0377e+00 28 1.0042e+00 -7.5276e-01 4.7743e-01 -2.7043e-02 4.8620e-01 -1.8925e-01 5.2803e-03 5.0000e-03
146 00:00:13 1.7435e+00 29 FP 1.0031e+00 -5.4722e-01 1.2499e-01 -6.4590e-04 4.4052e-01 -6.6222e-02 1.6599e-04 5.0000e-03
146 00:00:13 1.7434e+00 30 SN 1.0031e+00 -5.4722e-01 1.2499e-01 -6.4580e-04 4.4051e-01 -6.6219e-02 1.6597e-04 5.0000e-03
150 00:00:13 1.6502e+00 31 1.0033e+00 -4.5328e-01 5.3733e-02 -5.1083e-05 3.8151e-01 -3.1822e-02 1.6520e-05 5.0000e-03
159 00:00:13 1.4453e+00 32 EP 1.0160e+00 -7.9372e-02 4.6870e-05 -9.1827e-15 7.6929e-02 -4.2669e-05 7.6046e-15 5.0000e-03
the forcing frequency 9.9500e-01 is nearly resonant with the eigenvalue -2.5000e-04 + i1.0000e+00
the forcing frequency 9.9555e-01 is nearly resonant with the eigenvalue -2.5000e-04 + i1.0000e+00
the forcing frequency 9.9645e-01 is nearly resonant with the eigenvalue -2.5000e-04 + i1.0000e+00
.
.
.
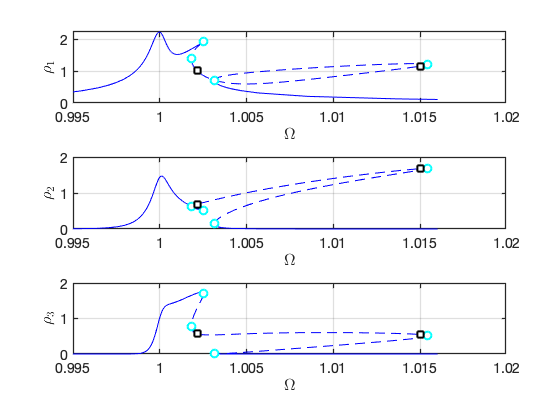
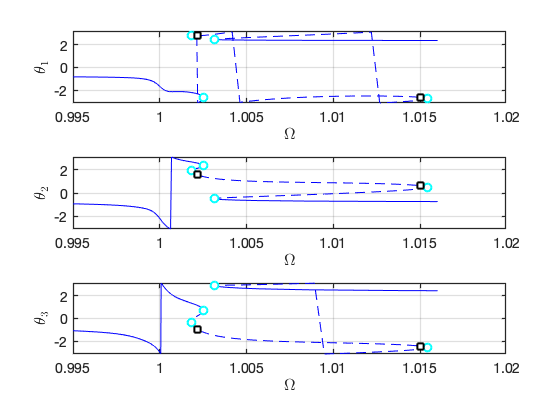
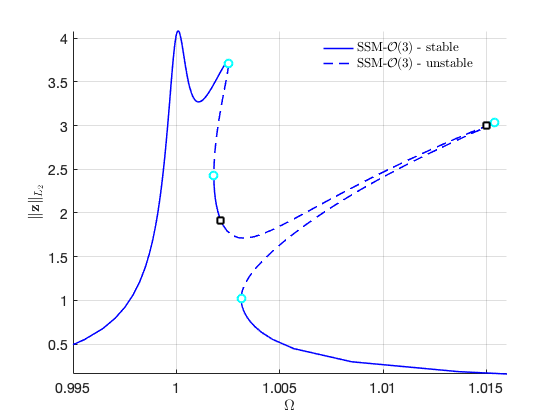
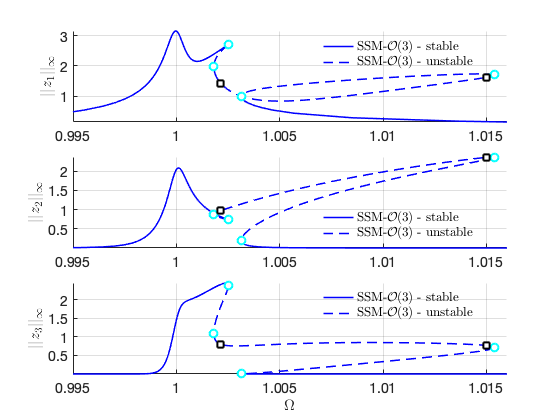
Validation using COCO
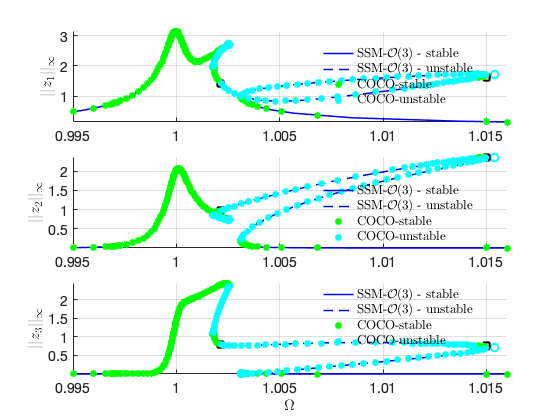
To conclude this example, we use the po-toolbox (collocation method) of COCO to validate the results obtained from the SSM analysis. As we can see, the results of the two methods match well. In addition, the runtime of collocation method is nearly three times of that of the SSM analysis.
nCycles = 100; coco = cocoWrapper(DS, nCycles, outdof); set(coco.Options, 'PtMX', 500); set(coco.Options, 'NAdapt', 1, 'h_max', 50); startcoco = tic; bd2 = coco.extract_FRC(freqRange); timings.cocoFRC = toc(startcoco)
Run='FRC': Continue primary family of periodic orbits.
STEP DAMPING NORMS COMPUTATION TIMES
IT SIT GAMMA ||d|| ||f|| ||U|| F(x) DF(x) SOLVE
0 1.00e-02 1.06e+01 0.0 0.0 0.0
1 1 1.00e+00 5.51e-01 3.11e-04 1.06e+01 0.0 0.0 0.0
2 1 1.00e+00 3.28e-01 5.04e-06 1.06e+01 0.0 0.1 0.0
3 1 1.00e+00 2.39e-03 8.14e-10 1.06e+01 0.0 0.1 0.0
4 1 1.00e+00 7.35e-07 2.21e-15 1.06e+01 0.0 0.1 0.0
STEP TIME ||U|| LABEL TYPE omega po.period eps amp1 amp2 amp3
0 00:00:00 1.0562e+01 1 EP 9.9697e-01 6.3023e+00 5.0000e-03 7.7455e-01 4.7293e-02 1.2789e-05
5 00:00:02 9.8080e+00 2 EP 9.9500e-01 6.3148e+00 5.0000e-03 4.9155e-01 8.4633e-03 4.5087e-08
STEP TIME ||U|| LABEL TYPE omega po.period eps amp1 amp2 amp3
0 00:00:02 1.0562e+01 3 EP 9.9697e-01 6.3023e+00 5.0000e-03 7.7455e-01 4.7293e-02 1.2789e-05
10 00:00:04 1.7768e+01 4 9.9893e-01 6.2899e+00 5.0000e-03 1.6913e+00 5.1904e-01 3.4088e-02
20 00:00:07 3.0203e+01 5 9.9960e-01 6.2857e+00 5.0000e-03 2.6730e+00 1.3558e+00 5.0318e-01
30 00:00:11 3.7130e+01 6 9.9987e-01 6.2840e+00 5.0000e-03 3.1038e+00 1.8723e+00 1.1275e+00
40 00:00:15 3.9609e+01 7 1.0001e+00 6.2827e+00 5.0000e-03 3.0893e+00 2.0777e+00 1.6289e+00
50 00:00:21 3.7485e+01 8 1.0003e+00 6.2811e+00 5.0000e-03 2.7028e+00 1.9393e+00 1.9053e+00
60 00:00:25 3.2974e+01 9 1.0008e+00 6.2784e+00 5.0000e-03 2.2082e+00 1.4730e+00 2.0285e+00
70 00:00:29 3.3298e+01 10 1.0016e+00 6.2731e+00 5.0000e-03 2.3053e+00 9.7043e-01 2.2682e+00
80 00:00:32 3.6158e+01 11 1.0024e+00 6.2683e+00 5.0000e-03 2.6430e+00 7.6530e-01 2.4544e+00
90 00:00:34 3.5127e+01 12 1.0025e+00 6.2678e+00 5.0000e-03 2.6703e+00 7.3846e-01 2.2577e+00
100 00:00:37 2.9457e+01 13 1.0020e+00 6.2707e+00 5.0000e-03 2.3453e+00 8.1607e-01 1.5991e+00
110 00:00:42 2.2086e+01 14 1.0019e+00 6.2712e+00 5.0000e-03 1.6877e+00 9.2365e-01 9.0151e-01
120 00:00:45 1.9050e+01 15 1.0043e+00 6.2561e+00 5.0000e-03 8.5905e-01 1.3293e+00 7.8705e-01
130 00:00:49 2.6164e+01 16 1.0110e+00 6.2146e+00 5.0000e-03 1.2724e+00 2.0835e+00 8.3858e-01
140 00:00:53 2.8886e+01 17 1.0138e+00 6.1974e+00 5.0000e-03 1.5401e+00 2.2993e+00 7.9331e-01
149 00:00:57 2.9873e+01 18 FP 1.0150e+00 6.1904e+00 5.0000e-03 1.7027e+00 2.3503e+00 7.0856e-01
150 00:00:57 2.9819e+01 19 1.0149e+00 6.1907e+00 5.0000e-03 1.7193e+00 2.3365e+00 6.8695e-01
160 00:01:01 2.7001e+01 20 1.0122e+00 6.2076e+00 5.0000e-03 1.6954e+00 2.0129e+00 4.6399e-01
170 00:01:04 2.0709e+01 21 1.0069e+00 6.2402e+00 5.0000e-03 1.4611e+00 1.2981e+00 1.7100e-01
180 00:01:09 1.3658e+01 22 1.0032e+00 6.2634e+00 5.0000e-03 1.0500e+00 2.6670e-01 2.2387e-03
182 00:01:10 1.2963e+01 23 FP 1.0031e+00 6.2636e+00 5.0000e-03 9.9340e-01 2.0003e-01 9.4307e-04
190 00:01:14 1.0315e+01 24 1.0044e+00 6.2558e+00 5.0000e-03 5.8781e-01 1.9034e-02 5.8181e-07
194 00:01:16 8.9454e+00 25 EP 1.0160e+00 6.1842e+00 5.0000e-03 1.5506e-01 8.6834e-05 1.5227e-14
Computation time:
Modal Analysis MD : 0.2106
SSM computation epPolarFRC: 56.2846
SSM computation epCartFRC : 42.7095
Full system cocoFRC : 83.4836